New Quantitative Constraints on Orographic Gravity Wave Stress and Drag

Abstract

Our project will utilize recent advances in the analysis of high-resolution satellite data for studies of the full three-dimensional (3D) properties of orographic gravity wave (OGW) events, and evaluation of existing and new parametrizations of OGW drag in global models. We will bring together an international team of experts on (1) the satellite data and their analysis, (2) high-resolution wave-resolving models, (3) global prediction models, and (4) parametrization methods.

OGW drag is one of the fundamental physics parametrizations employed in every global prediction model across timescales from weather to climate. Orographic waves are part of the complex dynamical interaction of winds with topography, and one piece in the puzzle that is topography's effect on global circulation. Parametrized OGW drag provides an important control on model wind biases at levels from the surface through the middle atmosphere, and these alterations in winds in turn affect stationary and synoptic Rossby wave propagation and dissipation. Thus properly tuned OGW drag parameterzations can improve weather model prediction skill from synoptic to seasonal timescales [Sigmond et al. 2013; Shaw et al. 2014]. Climate models have long relied on OGW drag for improved representations of both the mean climate and variability [Alexander et al. 2010]. In the stratosphere in particular, the circulation changes associated with OGW drag reduce winter temperature biases that affect ozone chemistry, so OGW drag is also fundamental to chemistry-climate modelling [Eyring et al. 2010]. Despite its importance in global models, OGW parametrization tuning is still only weakly constrained by observations in today's models, while new issues related to shortcomings in OGW parametrization are arising.

At ISSI Bern, we will perform the difficult task of determining uncertainties in existing observations and parametrization methods, and evaluating new state-of-the-art techniques for representing OGW drag in global models. Our members are all actively working on projects that will feed the team's joint work. Several members provide links to relevant international projects within the World Climate and World Weather Research Programmes (WCRP and WWRP), ensuring the team's results will be disseminated for broad scientific impact.

Figures:
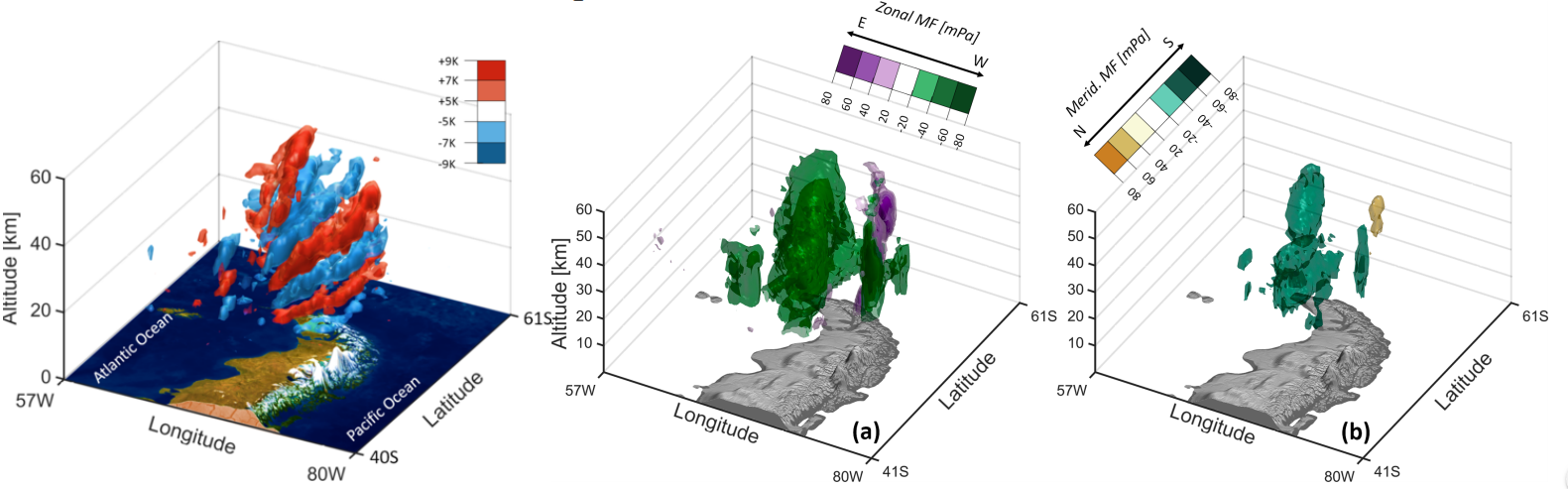
Top: Wright et al, ACP 2017
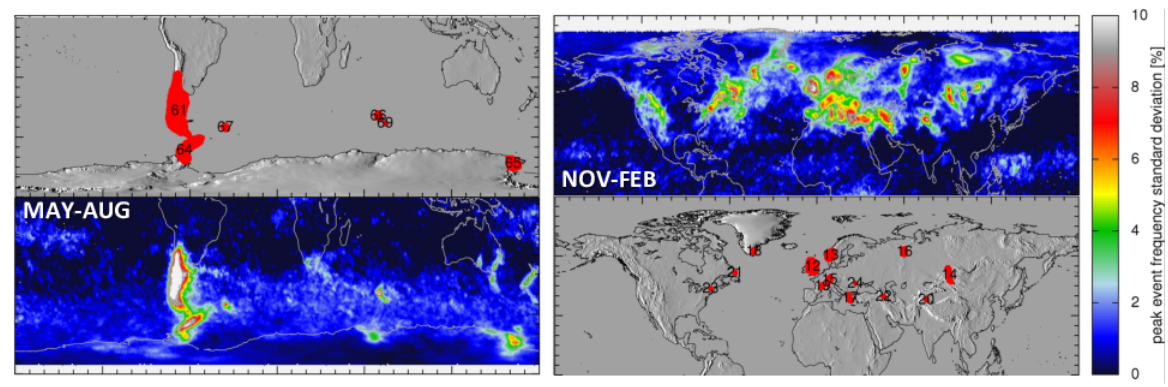
Middle: Hoffmann et al, JGR 2013
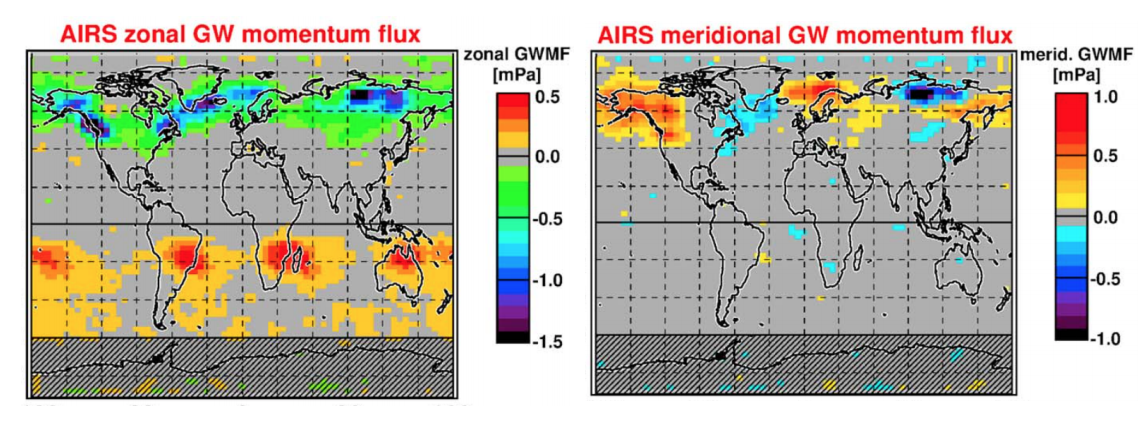
Bottom: Ern et al, GRL 2016

The Team

	Joan Alexander (Team Leader) Northwest Research Associates, Boulder, USA Website
	Julio Bacmeister National Center for Atmospheric Research, Boulder, USA Website
	Manfred Ern Forschungszentrum Juelich, Juelich, Germany Website
	Sonja Gisinger Deutsches Zentrum fuer Luft- und Raumfahrt, Wessling, Germany Website
	Laura Holt Northwest Research Associates, Boulder, USA Website
	Christopher Kruse National Center for Atmospheric Research, Boulder, USA Website
	Lars Hoffmann Forschungszentrum Juelich, Juelich, Germany Website
	Riwal Plougonven Ecole Polytechnique, Paris, France Website
	Inna Polichtchouk European Centre for Medium-Range Weather Forecasting, UK Website
	Petr Šácha University of Vigo, Vigo, Spain Website
	Kaoru Sato University of Tokyo, Tokyo, Japan Website
	Ryosuke Shibuya University of Tokyo, Tokyo, Japan Website
	Annelize van Niekerk Met Office, Exeter, UK Website
	Corwin Wright University of Bath, Bath, UK Website

Report on First Meeting

Publications

• Strube, C., Preusse, P., Ern, M., and Riese, M.
  Propagation paths and source distributions of resolved gravity waves in ECMWF-IFS analysis fields around the southern polar night jet
  Atmos. Chem. Phys.https://doi.org/10.5194/acp-21-18641-2021, 2021.
• Sacha, P., Kuchar, A., Eichinger, R., Pisoft, P., Jacobi, C., and Rieder, H. E.
  Diverse dynamical response to orographic gravity wave drag hotspots—a zonal mean perspective
  Geophys. Res. Lett.https://doi.org/10.1029/2021GL093305, 2021.
• Haruka Okui, Kaoru Sato, Dai Koshin and Shingo Watanabe
  Formation of a Mesospheric Inversion Layer and the Subsequent Elevated Stratopause Associated With the Major Stratospheric Sudden Warming in 2018/19
  J. Geophys. Res.https://doi.org/10.1029/2021JD034681, 2021.
• Inna Politchchouk, Nils Wedi and Young-Ha Kim
  Resolved gravity waves in the tropical stratosphere: Impact of horizontal resolution and deep convection parametrization
  Q. J. Roy. Met. Soc https://doi.org/10.1002/qj.4202, 2021.
• Annelize van Niekerk and Simon Vosper
  Towards a more "scale-aware" orographic gravity wave drag parametrization: Description and initial testing
  Q. J. Roy. Met. Soc https://doi.org/10.1002/qj.4126, 2021.
• Corwin J. Wright, Neil P. Hindley, M. Joan Alexander, Laura A. Holt, and Lars Hoffmann
  Using vertical phase differences to better resolve 3D gravity wave structure
  Atmos. Meas. Tech. https://doi.org/10.5194/amt-14-5873-2021, 2021.
• Wildmann, N., Eckert, R., Doernbrack, A., Gisinger, S., Rapp, M., Ohlmann, K., and van Niekerk, A
  Measurements of Wind and Turbulence by a Motor Glider in the Andes.
  J. Atmos. Ocean. Tech. https://doi.org/10.1175/JTECH-D-20-0137.1, 2021.
• M. Rapp et al
  SOUTHTRAC-GW: An airborne field campaign to explore gravity wave dynamics at the world’s strongest hotspot.
  Bull. Am. Met. Soc. https://doi.org/10.1175/BAMS-D-20-0034.1, 2020.
• R. Eichinger, H. Garny, and P. Šácha.
  Effects of missing gravity waves on stratospheric dynamics; Part 1: climatology.
  Clim. Dynam., https://doi.org/10.1007/s00382-020-05166-w, 2020.
• Eichinger, R and Šácha, P.
  Overestimated acceleration of the advective Brewer–Dobson circulation due to stratospheric cooling.
  QJR Meteorol Soc. https://doi.org/10.1002/qj.3876, 2020.
• I. Krisch, M. Ern, L. Hoffmann, P. Preusse, C. Strube, J. Ungermann, W. Woiwode, and M. Riese.
  Superposition of gravity waves with different propagation characteristics observed by airborne and space-borne infrared sounders.
  Atmos. Chem. Phys., https://doi.org/10.5194/acp-20-11469-2020/, 2020.
• A. Kuchar, P. Sacha, R. Eichinger, C. Jacobi, P. Pisoft and H.E. and Rieder
  On the intermittency of orographic gravity wave hotspots and its importance for middle atmosphere dynamics
  Weather Clim. Dynam., https://doi.org/10.5194/wcd-1-481-2020, 2020.
• R. Plougonven, A. de la Camara, A. Hertzog, and F. Lott.
  How does knowledge of atmospheric gravity waves guide their parameterizations?
  QJR Meteorol Soc., https://doi.org/10.1002/qj.3732, 2020.
• A. van Niekerk, I. Sandu, A. Zadra, E. Bazile, T. Kanehama, M. Köhler, MS Koo, HJ Choi, Y Kuroki, M Toy, SB Vosper and V Yudin.
  COnstraining ORographic Drag Effects (COORDE): a model comparison of resolved and parametrized orographic drag.
  J. Adv. Modeling Earth Sys., https://doi.org 10.1029/2020MS002160, 2020

Schedule