Electron Spectrum

It is well known [3] that the dominant X-ray emission mechanism during solar flares is collisional bremsstrahlung of electrons with the ions of the solar plasma. The relation between the measured optically thin
photon spectrum g(ε) and the mean electron flux spectrum f(E) is described by a Volterra integral equation of the first kind [4]:

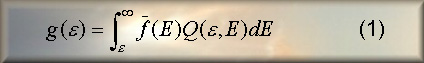
where Q(ε,E) is a suitable bremsstrahlung cross section for production of a photon of energy ε by an electron of energy E.
The linear inverse problem we are interested in, is the one to determine f(E) from a noisy sampled knowledge of g(ε). In a thick-target interpretation, the knowledge of f(E) provides the injected electron flux spectrum by means of numerical differentiation.
If addressed naively, the solution of Equation (1) may lead to very unstable and unphysical reconstructions of the electron spectra. A notable reduction of this numerical instability is typically obtained by means of the following different approaches:

1) Parametric forward-fitting [6]: a parametric form for f(E) is inserted into the integral at the right hand side of Equation (1) and the parameters are fixed by minimizing the distance from the experimental data.

2) Matrix inversion with data-adaptive binning [8]: Equation (1) is solved by standard square matrix row elimination and the electron spectrum is derived locally from the photon spectrum exploiting the fact that:

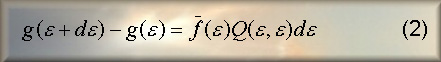
The inversion of Equation (1) is then stabilized by adjusting Q through judicious energy binning.

3) Tikhonov regularization theory [13]: a regularized solution of Equation (1) is obtained by solving the Tikhonov minimum problem:

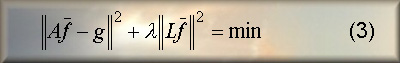
where A is the integral operator in Equation (1), L is an appropriate differential operator and λ is the so called regularization parameter providing an optimal trade-off between stability (measured by the second term at the left hand side of Equation (3)) and fitting (measured by the first term at the left hand side of Equation (3)). The computation of the minimum is performed by means of Singular Value Decomposition (SVD) techniques [1,2].

The problem of the inversion of Equation (1) has been already widely carried out by using the three methods separately [6,8,9,11,12], although a systematic comparison of the effectiveness of these three approaches has never been considered. We will perform such comparison by means of blind tests, whereby physically significant synthetic photon spectra will be inverted without knowing f(E) in advance.

Furthermore Equation (1) is a simplified model for the bremsstrahlung emission process in which we use a solid-angle-averaged cross section depending only on E and ε (isotropic assumption) and a mean electron flux differential only in E. However, in general, the correct cross section for bremsstrahlung photon emission depends also on the emission angle (θ) between the incoming electron and the emitted photon directions [5,7] and the electron flux is differential in E and in the solid angle Ω describing the incoming electron direction.
It follows that a more realistic model is given by:

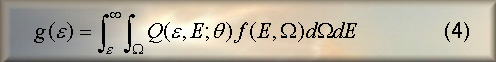
and a more interesting problem is the one to recover a function of two variables from the knowledge of a function of one variable (bivariate problem).

We have already faced the inversion of Equation (4) in the frame of the regularization theory by assuming f(E,Ω) separable in E and Ω (i.e. f(E,Ω)=F(E)h(Ω)) and we have recovered F(E) by choosing a suitable form for the angular dependence h(Ω) [10].
Even in presence of strong constraints, this approach showed how the angular dependence cannot be neglected: the use of anisotropic cross section yields to recovered electron spectra significantly different from the ones reconstructed by using the solid-angle-averaged cross section.

In this project we want to avoid the separability hypothesis and to recover f(E,Ω) directly from the X-ray spectra by assuming the most general anisotropic form for the integral kernel.

[1] Bertero M., De Mol C. and Pike E. R. 1985, Linear Inverse Problems with discrete data: I - General formulation and syngular system analysis, Inverse Problems 1, 300-330

[2] Bertero M., De Mol C. and Pike E. R. 1988, Linear Inverse Problems with discrete data: II - Stability and regularization, Inverse Problems 4, 573-594

[3] Brown J. C. 1971, The deduction of energy spectra of non-thermal electrons in flares from the observed dynamic spectra of hard X-ray bursts, Solar Physics 18, 489

[4] Brown J. C., Emslie A. G. and Kontar E. P. 2003, The determination and use of mean electron flux spectra in solar flares, ApJL 595, L115-L117

[5] Gluckstern R. L. and Hull M. H. 1953, Polarization Dependence of the Integrated Bremsstrahlung Cross Section, Physical Review 90, 1030

[6] Holman G. D., Sui L., Schwartz R. A. and Emslie A. G. 2003, Electron Bremsstrahlung Hard X-Ray Spectra, Electron Distributions and Energetics in the 2002 July 23 Solar Flare, ApJL 595, L97

[7] Koch H. W. and Motz J. W. 1959, Bremsstrahlung Cross-Section Formulas and Related Data, Rev. Mod. Phys. 31, 920-955

[8] Johns C. M. and Lin R. P. 1992, The Derivation of Parent Electron Spectra from Bremsstrahlung Hard X-ray Spectra, Solar Physics 137, 121

[9] Massone A. M., Piana M., Conway A. and Eves B. 2003, A regularization approach for the analysis of RHESSI X-ray spectra, A&A 405, 325-330

[10] Massone A. M., Emslie A. G., Kontar E. P., Piana M., Prato M. and Brown J. C. 2004, Anisotropic bremsstrahlung emission and the form of regularized electron flux spectra in solar flares, ApJ 613, 1233-1240.

[11] Piana M. 1994, Inversion of bremsstrahlung spectra emitted by solar plasma, A&A 288, 949-959

[12] Piana M., Massone A. M., Kontar E., Emslie A. G., Brown J. C. and Schwartz R. A. 2003, Regularized electron flux spectra in the July 23, 2002 solar flare, ApJL 595, L127-L130

[13] Tikhonov A. N. 1963, On solving ill-posed problems and method of regularization, Dokl. Akad. Nauk. USSR 153, 501-504

Home - Abstract - Team Members

Project - Events - Links