
ISSI Visiting Scientists Programme

RHESSI IMAGING
The process of image formation can be described by the integral equation [2]:
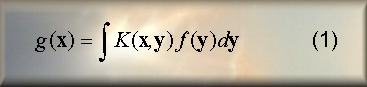
where g(x) is the recorded noisy image, f(y) is the original scene
and K(x,y) is the so called Point Spread Function (PSF) of the
imaging system. The effect of the PSF is called blurring and it
represents the image of a point source located at the point y (impulse
response function).
If the PSF is space invariant (i.e. K(x,y)=K(x-y)),
the image restoration problem becomes the deconvolution problem
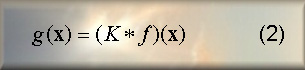
Since RHESSI imaging system [3] has nine rotating collimators, characterized by
nine different PSFs (and therefore by nine different resolutions and
signal-to-noise ratios) the RHESSI imaging problem reduces to a multiple
deconvolution problem, i.e., the problem of restoring an object using nine
different images of it. Our idea is to address such problem taking into account
the following methodological issues:
1. instead of summing up the images and using an averaged PSF, a better
resolution is achievable by appropriately combining the nine images and PSFs
according to the approach followed in [4];
2. a better accuracy is achievable by using a priori information on the
solution (such as its positivity or its compact support [5]) and on the
statistical properties of the noise affecting the data [1].
REFERENCES
[1] Anconelli B., Bertero M., Boccacci P. and Carbillet M. 2005, Restoration of
interferometric images IV: an algorithm for super-resolution of stellar systems,
A&A (in press)
[2] Bertero M. and Boccacci P. 1998, Introduction to inverse problems in imaging, IOP, Bristol
[3] Hurford G. J. et al. 2002, The RHESSI Imaging Concept, Solar Physics 210, 61-86
[4] Piana M. and Bertero M. 1995, Regularized deconvolution of multiple images of the same object, J. Opt. Soc. Am. A 13, 1516-1523
[5] Piana M. and Bertero
M. 1997, Projected Landweber method and preconditioning, Inverse Problems
13, 441-463
![]()
Site created and updated by Marco Prato
Comments and suggestions to: prato (at) dima.unige.it