ISSI Visiting Scientists Programme

RHESSI SPECTRA:

RECONSTRUCTION OF THE DIFFERENTIAL EMISSION MEASURE

Any interpretation of the mean electron flux spectrum f(E) requires model dependent assumptions. Under a purely thermal interpretation of the equation

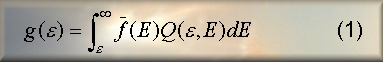
(see Rhessi spectra: reconstruction of the electron spectrum), it can be shown [1] that the equation

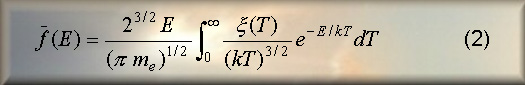
occurs, where T is the temperature, k is the Boltzmann constant and the differential emission measure ξ(T) is defined as:

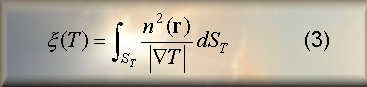
with n(r) the plasma density and S_T a constant temperature surface.

We observe that, in principle, the inversion of Equation (2) can be performed using the same Tikhonov method described for the non-thermal problem. However, the presence of the exponential function in the integral kernel increases dramatically the numerical instability of the problem and reduces significantly the effectiveness of any inversion approach.
Therefore, while, for the non-thermal problem, zero order (L=I) or first order (L=D) regularizations are equally effective, in the thermal model zero-order regularization does not assure a sufficient degree of smoothness and the choice of first order regularization becomes essential.
 

REFERENCES

[1] Brown J. C. 1974 in G. A. Newkirk (ed.), Coronal Disturbances, IAU Symp.  57, 395
 

Home  -  Abstract  -  Team Members  Project  -  Events  -  Links

Site created and updated by Marco Prato

Comments and suggestions to: prato (at) dima.unige.it