Comet Interceptor will pass through a potentially hazardous region of such a comet’s inner and outer coma. It is therefore important to assess the dust impact risk to the spacecraft and their scientific instruments to aid hazard mitigation strategies. Though models describing the dust environment for space missions are not new, the Comet Interceptor mission is unique. It is the first mission for which the mission’s precise target (a specific comet) could remain unknown until after launch. Naturally, this is a particular problem for determining the expected dust coma because of the many parameters with a broad range of possible values.
A Team led by team members Vladimir Zakharov and Raphael Marschall developed a new model to address this problem. By simulating tens of thousands of possible scenarios, they could statistically determine the scenarios the space mission could encounter. Figure 1 below shows the number of particles of a particular mass expected to hit the spacecraft during the encounter. The solid line shows the median and the different shaded areas the scatter in possible outcomes. The unknown properties of the comet of Comet Intercepter result in significant uncertainties that can be as large as four orders of magnitude. Once a comet has been chosen and characterised using ground-based telescopes, the relevant comet properties can be fed into the model to reduce uncertainties.
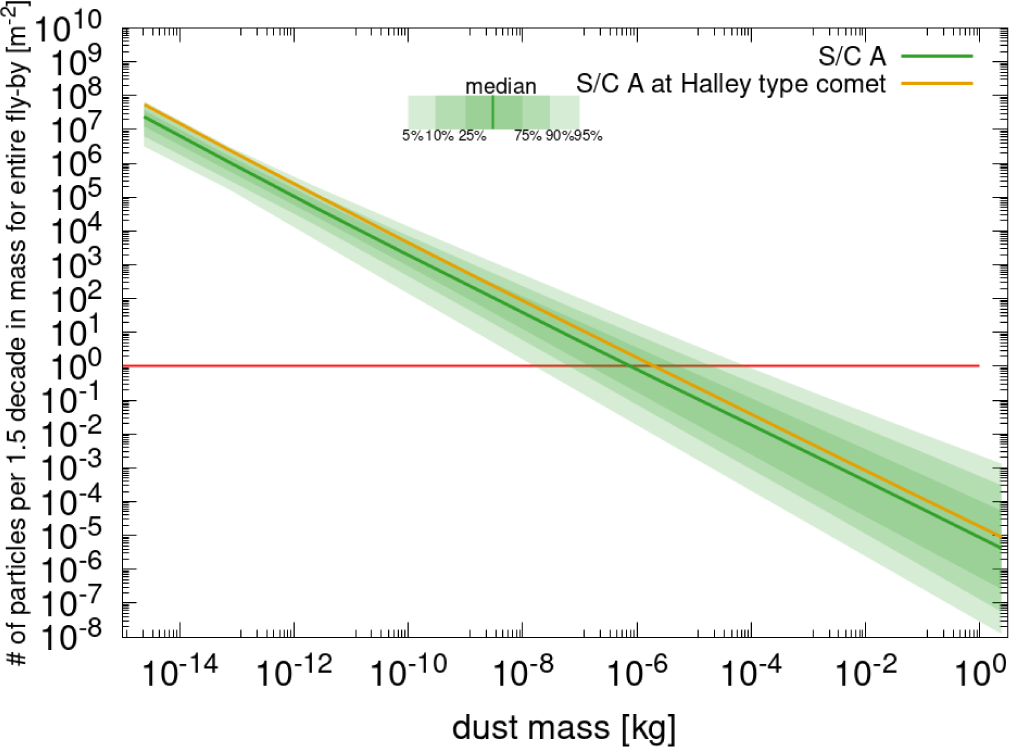
Figure 1: Total number of dust particles encountered according to the EDCM along the spacecraft trajectory of spacecraft A as function dust mass. The shaded areas show different percentile ranges within which cases fall. Additionally the orange curve shows the predicted median densities for a Halley type comet.
This new model also allowed the team to determine some fundamental properties of the activity of comets. One of the most accessible measurements that can be performed on a comet is to determine the brightness of the dust coma. This brightness is usually given in a quantity known as Afρ. Yet one would like to convert this brightness into a dust production rate at the comet’s surface. This most recent work shows that Afρ by itself is a bad predictor of the dust production rate. Yet, if, in addition, the dust’s size distribution can be measured, then we can derive relatively accurate values of the dust production rate from Afρ and the dust size distribution. This relationship is shown in Figure 2.
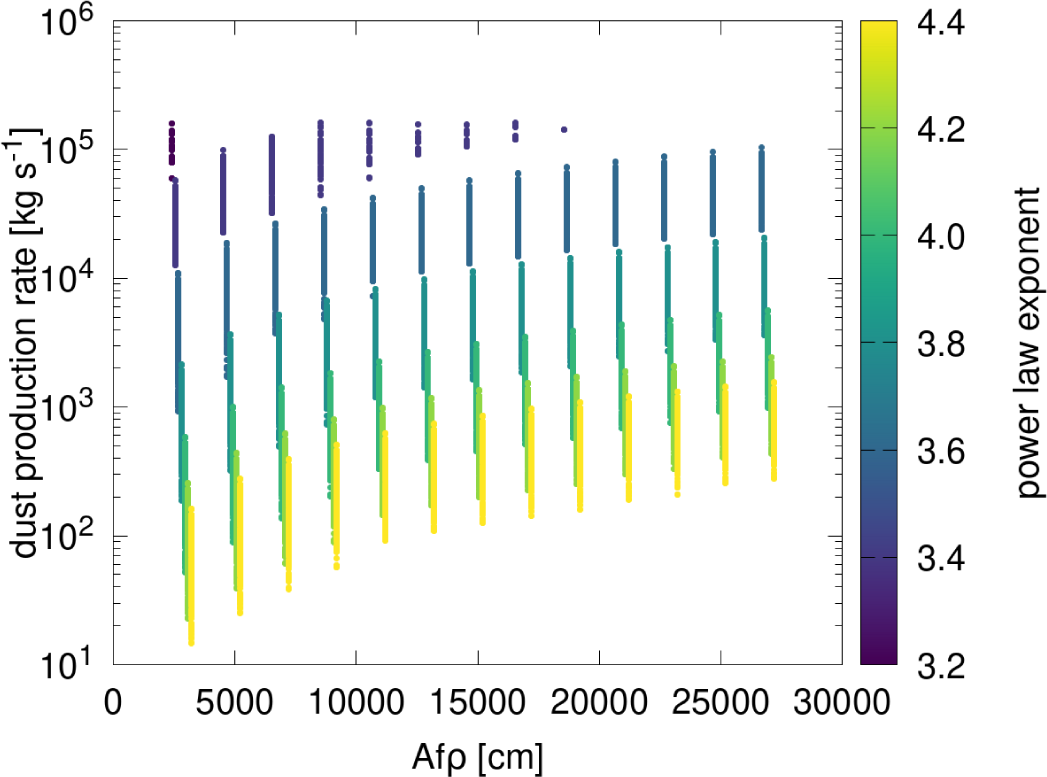
Figure 2: Dust production rate as a function of Afρ and the power law exponent, β, of the dust size distribution. The values of Afρ are slightly offset depending on the power law exponent to show the overlap resulting from β. By itself Afρ is a poor predictor of the dust production rate of a comet.
The model’s data is freely available on https://doi.org/10.5281/zenodo.6906815, and the paper Determining the dust environment of an unknown comet for a spacecraft flyby: The case of ESA’s Comet Interceptor mission is published in Astronomy & Astrophysics and is open access (https://doi.org/10.1051/0004-6361/202243648).



